Polygon

Demonstration of the line clipping routine

I had already published a vector graphics demo in 1990, but the routines for the lines and the rotation of the objects were all coded in assembler with absolute addressing (using GMON) and not with relative addresses (e.g. when you use labels in Maxam and compile to finished program). Thus I couldn't easily modify the routines or transfer them to any other program. The assembler GMON I had used for several years was pretty bad and when I switched over to Maxam I started to create a new vector graphics program. This time I wanted to improve the routines, so that I could also move the objects outside of the screen and that the invisible faces wouldn't be displayed.

Rotating cube with 8 bit calculation

First of all I created a line routine that was able to do clipping. The term clipping refers to the fact that one or both end points of the line could lie outside the visible screen area or any rectangular area. There are interpolation routines with which you can calculate at what exact x- and y-position the line will enter the screen when it is drawn from a start point outside the screen.

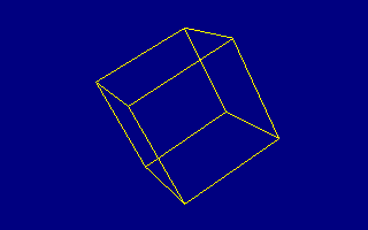
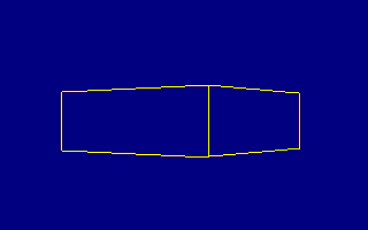
After that I started to write the routines that rotate polygons on the screen. Actually I didn't really use polygons, I created my own kind of data array to hold the points and the edges of the vector graphics and had custom routines to create the rotation. Several months later I learned how to use matrices to do this calculation a lot easier, but by then I was programming on the Acorn RiscPC and not on the CPC anymore. But that's a different story.

The first rotating object I had created was of course a cube. Since I used 8 Bit division instead of 16 Bit the calculation of the corners of my polygons was flawed and produced a lot of rounding errors. So the rotation doesn't really look good. 16 Bit rotation is just so much more complex and I wanted to save time and unused registers...

Removal of invisible surfaces

The next thing I did was to write a program that was able to identify the invisible surfaces of the object. Whether a surface is invisible or not can be determined if you calculate a vector that's pointing away from the surface in a 90 degrees angle and if that vector has a negative value on the z-axis. I've tried this in a second program where a small box is just rotating around the y-axis and where the surfaces can easily be removed. If you rotate an object around all three axes there are situations where this vector calculation doesn't function flawlessly, that is where surfaces are being painted that shouldn't be visible. Removing these as well includes some more complicated calculations that I didn't knew at that time.

I continued to explore vector graphics a little longer on the CPC. One of the results of this exploration was the fractal mountain routine that's presented somewhere else on this page. I should have done more with the line and filled triangle routines that I developed. But these routines had some errors that where hard to fix and since I went away to study I didn't have the time to continue with this.