| Home |
|
Amstrad |
|
Introduction Odiesoft demos Odiesoft games CPC Party pictures Downloads |
| Anime |
| Party pictures |
| Guestbook |
| Links |
| Contact |
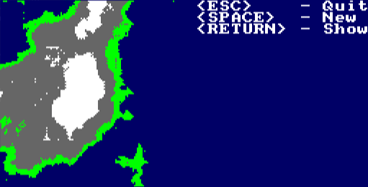
Fractal Mountain1994 | |||
I learned more about matrices and vector products, but I also wrote clipping routines for lines that had start and/ or end points out of the visible screen area. Additional to that I spend a lot of time creating and optimizing routines for filled triangles. As some of you may still remember, games like Starstrike 2 and Hard Driving demonstrated that the CPC was able to display fast, filled vector graphics. Knowing this I reasoned that there must be some sort of optimization technique to push the CPC to its limits in displaying quick filled vector graphics. After a lot of work I had created an optimized routine to create filled triangles that had no ristrictions whatsoever, that is all the edges were able to be outside a pre-defined rectangular area (e.g. the border of the screen) and yet the remaining area of the triangle would still be displayed correctly, clipped on some sides. This routine was comparatively fast, but I had the feeling that it still was no match for the Starstrike II routines. Anyway, I was happy with this first fully running version and I wrote a small test program to show the available positibilities with this filled triangles routine.
Due to memory and speed limitations the area that was being used as buffer for the fractal data was just 64*64 pixles. This fractal program started by setting random heights for each of the four corners of this area and then interpolated the points in between. This was achieved by dividing the distance between two already calculated points (points A and B) by two, thus getting a new point (C). Then the height for this point C was computed by taking the mean of the heights of the two starting points A and B and adding/ subtracting a random number that was depending on the iteration depth. This height served as the Y-coordinate for the polygon (the X axis was displayed horizontally on the screen from the left to the the right, the Y-axis was displayed vertically on the screen and the Z axis was parallel to view vector) and was also used to define the color of any triangle including this point as on of its three edges. The mean of the height of the three edges plus/ minus a random value defined whether the triangle would be white for snow, green for grass or blue for the lake/ water at the base of the mountains.
Besides this demonstration program for my filled vector graphics I didn't create any other vector programms on the CPC. On the RiscPC (that I usually used to develop vector graphics routines (because it was easier on the Risc PC with sixteen 32-bit registers compared to the six CPC 16 bit (BC, DE, HL and BC', HL' and DE') and two 8-bit registers (A and A'))) I actually wrote a small 3d world system using a mixture of BASIC (for the matrix calculation) and Assembler routines (for the filled triangles). I never ported this programm to the CPC though. Working and studying started to demand more and more time of me, so that there wasn't this much time left for CPC programming (which takes a LOT of time as some of you surely know). Thus this fractal mountain program remains as the only hint at what would have been possible on the CPC if I had had the time to continue my efforts...
| |||
| |||
|
last updated on Monday, Mai 19. 2003 by Odiesoft
|